Evolving Fuzzy Neural Network (EFuNN)

EFuNN Structure

EFuNN is a five neuron layer feed forward network (Figure 1), where each layer performs a specific function. The first neuron layer is the input layer. The second layer is the condition layer. Each neuron in this layer represents a single triangular fuzzy membership function (MF) attached to a particular input, and performs fuzzification of the input values based on that MF. This layer is not fully connected to the input layer, as each condition neuron is connected to a single input neuron, that is, each input neuron is connected to its own subset of condition neurons. The weight of the connection between the condition neuron and its input defines the centre of the condition neuron's MF, where the lower and upper bounds of the MF are defined as the centres of the neighbouring MF.

Structure of the Evolving Fuzzy Neural Network EFuNN
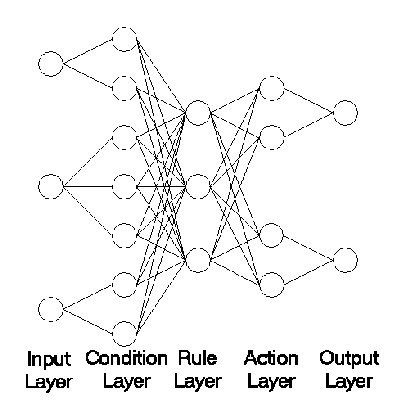
Figure 1 - structure of EFuNN. This figure shows an idealised EFuNN with three input neurons. Two MF are attached to the first input neuron, three to the second, and two to the third. There are three rule neurons and two outputs, with two MF attached to each output.

The activation function for a condition neuron c, which is based on triangular membership functions, is defined as:

$A_{c} = {\begin{matrix} 1 - \frac{I_{i} - W_{i, c}}{W_{i, c + 1} - W_{i, c}}, W_{i, c} < I_{i} < W_{i, c + 1} \\ 1 - \frac{W_{i, c} - I_{i}}{W_{i, c} - W_{i, c - 1}}, W_{i, c} < I_{i} < W_{i, c} \\ 1, W_{i, c} = I_{i} \\ 0, otherwise \end{matrix}$

Where:

$A_{c}$ is the activation of the condition neuron $c$

$W_{i, c}$ is the connection weight defining the centre of the MF attached to condition neuron $c$

$W_{i, c - 1}$ is the connection weight defining the centre of the MF to the left of $c$

$W_{i, c + 1}$ is the connection weight defining the centre of the MF to the right of $c$

$I$ is the input vector

The third layer of neurons is the evolving layer, which is also referred to as the rule layer. The distance measure used in this layer, which is the distance between the fuzzified input vector and the weight vector, is defined as:

$D_{n}$ = $\frac{\frac{1}{2} (\sum_{i = 1}^{c} ∣ I_{i} - W_{i, n} ∣)}{\sum_{i = 1}^{c} W_{i, n}}$

Where:

$A_{o}$ is the activation of the output node $o$

$A_{a}$ is the activation of the action node $a$

$m$ is the number of actiion neurons attached to $o$

$W_{o, a}$ is the value of the connection weight from action node $a$ to output $o$

The fourth layer of neurons is the action layer: neurons in this layer represent fuzzy membership functions attached to the output neurons. This layer is similar to the input layer, in that each action neuron is connected only to the output neuron with which its membership function is associated. Also, the value of the connection weight connecting the action neuron to its output defines the centre of the action neuron's membership function. The activation function of the action layer neurons is a simple saturated linear function. The final neuron layer is the output layer. This calculates crisp output values from the fuzzy output values produced by the action layer neurons. The output layer performs centre of gravity defuzzification over the action layer activations to produce a crisp output. This value is calculated according to:

$A_{o} = \frac{\sum_{a = i}^{m} W_{o, a} A_{a}}{\sum_{} A_{a}}$

Where:

$A_{i}$ is the activation of the output node $o$

$A_{a}$ is the activaiton of the action node $a$

$m$ is the number of action neurons attached to $o$

$W_{o, a}$ is the value of the connection weight from cation node $a$ to output $o$

The general ECoS learning algorithm is used to train EFuNN. The input vector is the fuzzified example input vector and the output vector is the fuzzified example output vector.

Fuzzy Rule Extraction

The algorithm for extracting Zadeh-Mamdani fuzzy rules from a trained EFuNN is as follows:

for each evolving layer neuron $h$ do

Create a new rule $r$

for each in put neuron $i$ do

Find the condition neuron $c$ with the largest weight $W_{c, h}$

Add antecedent to $r$ of the form " $i$ is $c$ $W_{c, h}$ " where ${Wc, h}_{}$ is the confidence factor for that antecedent

end for

for each output neuron $o$ do

Find the action neuron $a$ with th elargest weight $W_{h, a}$

Add a consequent to $r$ of the form " $o$ is $a$ $W_{h, a}$ where $W_{h, a}$ is the confidence factor for that consequent

end for

In a nutshell, this algorithm treats each evolving layer neuron as a fuzzy rule, and finds the connections with the largest weights. Since the connection weights in EFuNN represent fuzzified input and output vectors, by selecting the winning weights, the algorithm is finding the MF that the example values best fit.

The problem with this algorithm is that the MF in EFuNN are fixed and do not learn during training. So, if the MF were less than optimal, there will be less than optimal rules.

Maintained by Dr Michael J. Watts