ECoS Algorithms

Introduction

This page will introduce the basic structure of ECoS networks and the ECoS learning algorithm. At the moment, only algorithms that are included in the ECoS Toolbox are described here. More algorithms will be added presently.

ECoS Structure

An ECoS network is a multiple neuron layer, constructive artificial neural network. An ECoS network will always have at least one "evolving" neuron layer. This is the constructive layer, the layer that will grow and adapt itself to the incoming data, and is the layer with which the learning algorithm is most concerned. The meaning of the connections leading into this layer, the activation of this layer's neurons and the forward propagation algorithms of the evolving layer all differ from those of classical connectionist systems such as MLP. For the purposes of this paper, the term "input layer" refers to the neuron layer immediately preceding the evolving layer, while the term "output layer" means the neuron layer immediately following the evolving layer. This is irrespective of whether or not these layers are the actual input or output layers of the network proper. A generic ECoS structure is shown below:

General ECoS architecture

The "input layer" could be the input layer proper of the network (as with SECoS networks) or it could be a neuron layer that processes the actual input values for presentation to the evolving layer (as with EFuNN networks). By the same token, the "output layer" could be the actual output layer of the network (as it is with SECoS) or a neuron layer that further processes the outputs of the evolving layer (as with EFuNN). The connection layers from the input neuron layer to the evolving neuron layer and from the evolving layer to the output neuron layer, are fully connected.

The activation

A_{n}

of an evolving layer neuron

n

is determined by:

$A_{n} = 1 - D_{n}$

Where:

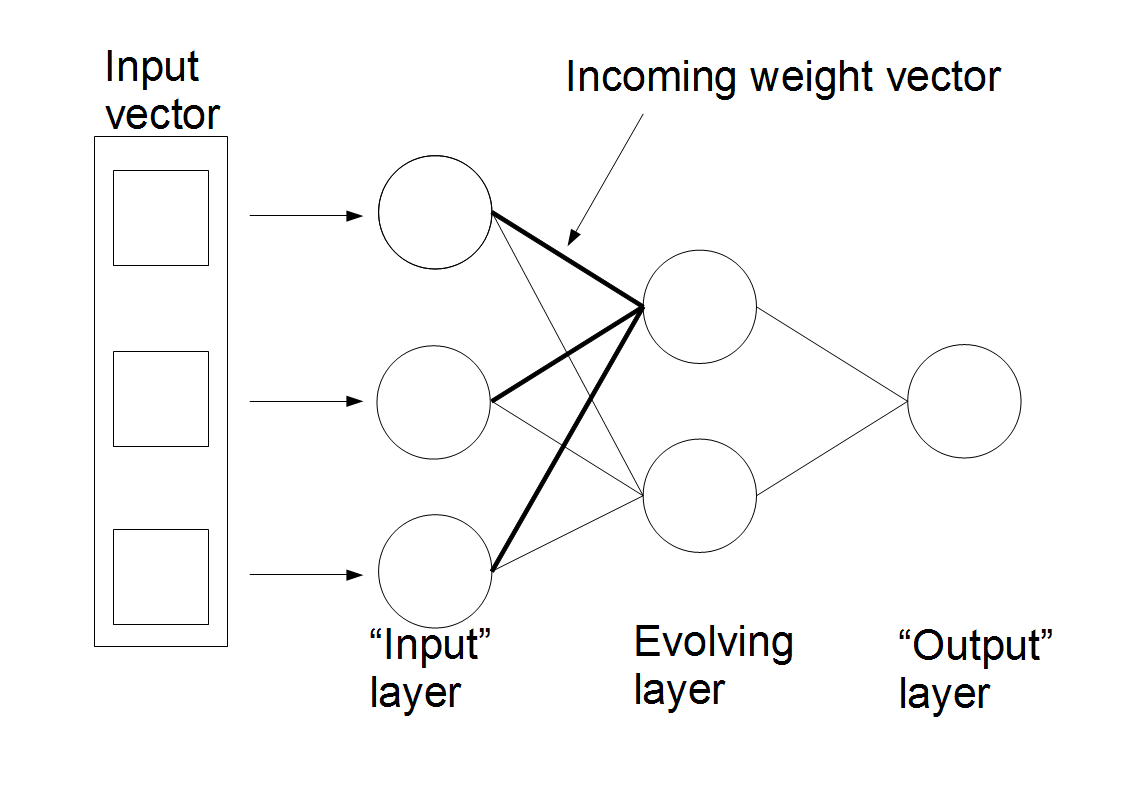
$D_{n}$ is the distance between the input vector and the incoming weight vector for that neuron.

Since ECoS networks are fully connected, it is possible to measure the distance between the current input vector and the incoming weight vector of each evolving-layer neuron. Although the distance can be measured in any way that is appropriate for the inputs, this distance function must return a value in the range of zero to unity. For this reason, most ECoS algorithms assume that the input data will be normalised, as it is far easier to formulate a distance function that produces output in the desired range if it is normalised to the range zero to unity.

Whereas most ANN propagate the activation of each neuron from one layer to the next, ECoS evolving layers propagate their activation by one of two alternative strategies. The first of these strategies, entitled OneOfN propagation, involves only propagating the activation of the most highly activated ("winning") neuron. The second strategy, ManyOfN propagates the activation values of those neurons with an activation value greater than the activation threshold $A_{thr}$ .

ECoS Learning

The ECoS learning algorithm is based on accommodating new training examples within the evolving layer, by either modifying the weight values of the connections attached to the evolving layer neurons, or by adding a new neuron to that layer. The algorithm employed is:

for each input vector

I

and its desired output vector

O_{d}

Propagate $I$ through the network

Find the most activated evolving layer neuron $j$ and its activation $A_{j}$

if $A_{j} < S_{thr}$ then

Add a neuron

else

Update the connections to the winning evolving layer neuron $j$

end if

The addition of neurons to the evolving layer is driven by the novelty of the current training example: if the current example is particularly novel (it is not adequately represented by the existing neurons) then a new neuron will be added. Four parameters are involved in this algorithm: the sensitivity threshold $S_{thr}$ , the error threshold $E_{thr}$ , and the two learning rates $l_{1}$ and $l_{2}$ . The sensitivity threshold and error threshold both control the addition of neurons and when a neuron is added, its incoming connection weight vector is set to the input vector is, and its outgoing weight vector is set to the desired output vector $O_{d}$ . The sensitivity and error thresholds are measures of the novelty of the current example. If the current example causes a low activation (that is, it is novel with respect to the existing neurons) then the sensitivity threshold will cause a neuron to be added that represents that example. If the example does not trigger the addition of a neuron via the sensitivity threshold, but the output generated by that example results in an output error that is greater than the error threshold (that is, it had a novel output), then a neuron will be added. The incoming weight vector of a new neuron is set to the current input vector. The outgoing weight vector of a new neuron is set to the current output vector.

The weights of the connections from each input $i$ to the winning neuron $j$ are modified according to the following equation:

$W_{i, j} (t + 1) = W_{i, j} (t) + l_{1} (I_{i} - W_{i, j} (t))$

Where:

$W_{i . j} (t)$ is the connection weight from input $i$ to $j$ at time $t$
$I_{i}$ is the $i$ th component of the input vector $I$

The weights from neuron $j$ to output $o$ are modified according to the following equation:

$W_{j, o} (t + 1) = W_{j, o} (t) + l_{2} A_{j} E_{o}$

Where:

$W_{j, o}$ is the connection weight from $j$ to output $o$ at time $t$
$A_{j}$ is the activation of $j$
$E_{o}$ is the error at $o$ , as measured according to the following equation:

$E_{o} = O_{o} - A_{o}$

Where:

$O_{o}$ is the desired activation value of output $o$
$A_{o}$ is the actual activation of $o$

Maintained by Dr Michael J. Watts